Shortest Path: Algorithm Class Notes

Mobiprep has created last-minute notes for all topics of Algorithm to help you with the revision of concepts for your university examinations. So let’s get started with the lecture notes on Algorithm.

1. Algorithm Basics

2. Divide And Conquer

3. Greedy Algorithm

4. Dynamic Programming

5. Shortest Path

6. Backtracking

7. Minimum Spanning Tree

8. Maximum Flow

9. Complexity Classes

Our team has curated a list of the most important questions asked in universities such as DU, DTU, VIT, SRM, IP, Pune University, Manipal University, and many more. The questions are created from the previous year's question papers of colleges and universities.

1. Explain Single Source Shortest Paths in a directed acyclic graph?

2. Explain Negative Weight Edges ?

3. Explain Dijkstra's Algorithm? Advantages and Disadvantages.

4. Explain Bellman-Ford Algorithm?

5. Explain All-Pairs Shortest Paths.

6. Explain Floyd-Warshall Algorithm.

7. Explain Johnson's Algorithm?

Shortest Path

Question- 1) Explain Single Source Shortest Paths in a directed acyclic graph?

Answer: A directed Acyclic graph is a graph with directed edges and no cycles. We can calculate single source shortest distances in O(V+E) time for Directed Acyclic Graphs where V is the number of nodes and E is the number of edges present in the graph. The idea is to use topological sorting.

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge ab, vertex a comes before b in the ordering.

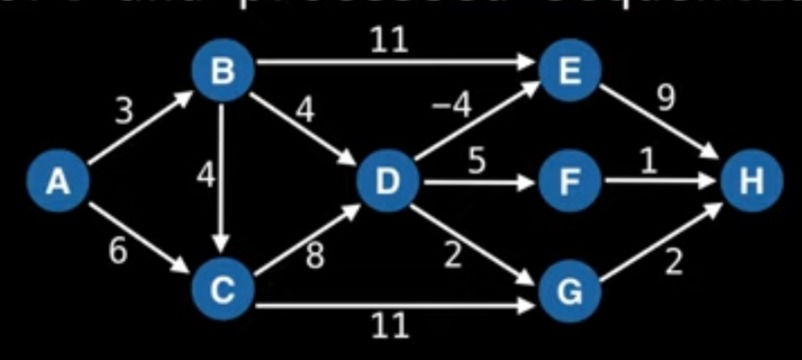
Consider an example:

Consider the above diagram. The objective is to find the minimum distance between point A and H. To achieve this, we will use topological sorting.

∞	∞	∞	∞	∞	∞	∞	∞
A	​B	C	D	E	​F	G	H

Now start with A and explore all the possible nodes and choose the minimum edge weight node. Initially like from A we can explore B and C and among them B have the minimum weight edges so we will choose that.

0	3	∞	∞	∞	∞	∞	∞
A	B	C	D	E	F	G	H

Now we can observe that from B as well as from A we can explore c so we will choose minimum as A-C is 6 and A-B-C is 7 so we will choose c

0	3	6	∞	∞	​∞	∞	∞
A	B	C	D	E	F	G	H

Repeat the process until you reach the end point i.e. H

0	3	6	7	∞	∞	∞	∞
A	B	C	D	E	F	G	H

0	3	6	7	3	∞	∞	∞
A	B	C	D	E	F	G	H

0	3	6	7	3	12	∞	∞
A	B	C	D	E	F	G	H

0	3	6	7	3	12	9	∞
A	B	C	D	E	F	G	H

0	3	6	7	3	12	9	11
A	B	C	D	E	F	G	H

So, the single source shortest paths between A and H in a directed acyclic graph give above is of weight 11.

i.e. A->B->D->G->H

Code implementation:

// C++ program to find single source shortest paths for Directed Acyclic Graphs
#include<iostream>
#include <bits/stdc++.h>
#define INF INT_MAX
usingnamespacestd;

// Graph is represented using adjacency list. Every node of adjacency list
// contains vertex number of the vertex to which edge connects. It also
// contains weight of the edge
classAdjListNode
{
intv;
intweight;
public:
AdjListNode(int_v, int_w) { v = _v; weight = _w;}
intgetV() { returnv; }
intgetWeight() { returnweight; }
};

// Class to represent a graph using adjacency list representation
classGraph
{
intV; // No. of vertices'

// Pointer to an array containing adjacency lists
list<AdjListNode> *adj;

// A function used by shortestPath
voidtopologicalSortUtil(intv, boolvisited[], stack<int>&Stack);
public:
Graph(intV); // Constructor

// function to add an edge to graph
voidaddEdge(intu, intv, intweight);

// Finds shortest paths from given source vertex
voidshortestPath(ints);
};

Graph::Graph(intV)
{
this->V = V;
adj = newlist<AdjListNode>[V];
}

voidGraph::addEdge(intu, intv, intweight)
{
AdjListNodenode(v, weight);
adj[u].push_back(node); // Add v to u's list
}

voidGraph::topologicalSortUtil(intv, boolvisited[], stack<int>&Stack)
{
// Mark the current node as visited
visited[v] = true;

// Recur for all the vertices adjacent to this vertex
list<AdjListNode>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
{
AdjListNode node = *i;
if(!visited[node.getV()])
topologicalSortUtil(node.getV(), visited, Stack);
}

// Push current vertex to stack which stores topological sort
Stack.push(v);
}

// The function to find shortest paths from given vertex. It uses recursive
// topologicalSortUtil() to get topological sorting of given graph.
voidGraph::shortestPath(ints)
{
stack<int> Stack;
intdist[V];

// Mark all the vertices as not visited
bool*visited = newbool[V];
for(inti = 0; i< V; i++)
visited[i] = false;

// Call the recursive helper function to store Topological Sort
// starting from all vertices one by one
for(inti = 0; i< V; i++)
if(visited[i] == false)
topologicalSortUtil(i, visited, Stack);

// Initialize distances to all vertices as infinite and distance
// to source as 0
for(inti = 0; i< V; i++)
dist[i] = INF;
dist[s] = 0;

// Process vertices in topological order
while(Stack.empty() == false)
{
// Get the next vertex from topological order
intu = Stack.top();
Stack.pop();

// Update distances of all adjacent vertices
list<AdjListNode>::iterator i;
if(dist[u] != INF)
{
for(i = adj[u].begin(); i != adj[u].end(); ++i)
if(dist[i->getV()] >dist[u] + i->getWeight())
dist[i->getV()] = dist[u] + i->getWeight();
}
}

// Print the calculated shortest distances
for(inti = 0; i< V; i++)
(dist[i] == INF)? cout<< "INF ": cout<<dist[i] << " ";
}

// Driver program to test above functions
intmain()
{
// Create a graph given in the above diagram. Here vertex numbers are
// 0, 1, 2, 3, 4, 5 with following mappings:
// 0=r, 1=s, 2=t, 3=x, 4=y, 5=z
Graph g(6);
g.addEdge(0, 1, 5);
g.addEdge(0, 2, 3);
g.addEdge(1, 3, 6);
g.addEdge(1, 2, 2);
g.addEdge(2, 4, 4);
g.addEdge(2, 5, 2);
g.addEdge(2, 3, 7);
g.addEdge(3, 4, -1);
g.addEdge(4, 5, -2);

ints = 1;
cout<< "Following are shortest distances from source "<< s <<" n";
g.shortestPath(s);

return0;
}

---

Question- 2) Explain Negative Weight Edges ?

Answer: An edge is (together with vertices) one of the two basic units out of which graphs are constructed. Each edge has two (or in hypergraphs, more) vertices to which it is attached, called its endpoints. Edges may be directed or undirected, Positive or negative. Negative edges are used to represent deprivation or the negative aspect of a graph.

Negative edges represent loss in real world scenario.

Consider an example, a person visited multiple cities. The edges represent the profit or loss the person undergoes while visiting one city from another depending on various factors.

Consider the value of graph in thousands. From the above graph we can say that if the person travels from A to B he gets a profit of 8000 whereas if a person moves from G to C it suffers a loss of 1000.

So, we can say that negative edges signify something opposite to the natural meaning.

---

Question- 3) Explain Dijkstra's Algorithm? Advantages and Disadvantages.

Answer: Dijkstra's Algorithm is a shortest path algorithm used to find the shortest path from source to all the possible vertex present in the graph. The algorithm used greedy approach to solve this problem. It is one of the most efficient algorithms but is not efficient to deal with negative weighted graph

The time complexity for all V vertices is V * (E*logV) i.eO(VElogV).

Pseudo code :

Input: Graph G, source vertex s, w (the weight of the edge)

Output: Shortest distance between source s and destination

Notation:

G =Weighted directed graph

S= Set of vertices

w (u, v) = the weight of the edge between u and v

s=source vertex

DIJKSTRA (G, w, s)
Initialize-single source (G, s)
S=Φ
Q=G.V
While Q !=Φ
U=EXTRACT-MIN(Q)
S=S U {u}
for each vertex v € G.Adj[u]
RELAX(u,v,w)

Consider the below graph:

We will be using Dijkstra's algorithm to find the shortest distance from vertex V1 to all other.

V1	V2	V3	V4	V5	V6
0	∞	∞	∞	∞	∞

As our starting vertex is V1 so choose V1 and explore all the possible vertex that can be accessed through V1

V2	V3	V4	V5	V6
2	4	∞	∞	∞

Now among these the smallest one is V2 so select V2. And explore all vertex and if it can relax any vertex with less value than replace that value. We can observe that V3 can be reached through v2 with total weight 2+1=3

V2	V3	V4	V5	V6
2	3	9	∞	∞

Now select V2

V2	V3	V4	V5	V6
2	3	9	6	∞

Now Select the minimum in all unselected vertex.

V2	V3	V4	V5	V6
2	3	8	6	11

Now select V4

V2	V3	V4	V5	V6
2	3	8	6	11

Now select V4

V2	V3	V4	V5	V6
2	3	8	6	9

Now select 6

V2	V3	V4	V5	V6
2	3	8	6	9

So, the result is

Vertex	Distance
V2	2
V3	3
V4	8
V5	6
V6	9

Advantages: -

1) Implemented in many used applications like Google Maps.

2) It is used in finding Shortest Path.

3) To find locations of Map which refers to vertices of graph.

4) Distance between the location refers to edges.

5) It is used in IP routing to find Open shortest Path First.

6) It is used in the telephone network.

Disadvantages: -

1) It does blind search so wastes lot of time while processing.

2) It cannot handle negative edges.

3) This leads to acyclic graphs and most often cannot obtain the right shortest path.

Code Implementation:

// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph

#include <limits.h>
#include <stdio.h>

// Number of vertices in the graph
#define V 9

// A utility function to find the vertex with minimum distance value, from
// the set of vertices not yet included in shortest path tree
intminDistance(intdist[], boolsptSet[])
{
// Initialize min value
intmin = INT_MAX, min_index;

for(intv = 0; v < V; v++)
if(sptSet[v] == false&&dist[v] <= min)
min = dist[v], min_index = v;

returnmin_index;
}

// A utility function to print the constructed distance array
voidprintSolution(intdist[])
{
printf("Vertex \t\t Distance from Source\n");
for(inti = 0; i< V; i++)
printf("%d \t\t %d\n", i, dist[i]);
}

// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
voiddijkstra(intgraph[V][V], intsrc)
{
intdist[V]; // The output array. dist[i] will hold the shortest
// distance from src to i

boolsptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized

// Initialize all distances as INFINITE and stpSet[] as false
for(inti = 0; i< V; i++)
dist[i] = INT_MAX, sptSet[i] = false;

// Distance of source vertex from itself is always 0
dist[src] = 0;

// Find shortest path for all vertices
for(intcount = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices not
// yet processed. u is always equal to src in the first iteration.
intu = minDistance(dist, sptSet);

// Mark the picked vertex as processed
sptSet[u] = true;

// Update dist value of the adjacent vertices of the picked vertex.
for(intv = 0; v < V; v++)

// Update dist[v] only if is not in sptSet, there is an edge from
// u to v, and total weight of path from srcto v through u is
// smaller than current value of dist[v]
if(!sptSet[v] && graph[u][v] &&dist[u] != INT_MAX
&&dist[u] + graph[u][v] <dist[v])
dist[v] = dist[u] + graph[u][v];
}

// print the constructed distance array
printSolution(dist);
}

// driver program to test above function
intmain()
{
/* Let us create the example graph discussed above */
intgraph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };

dijkstra(graph, 0);

return0;
}

---

Question- 4) Explain Bellman-Ford Algorithm?

Answer: Bellman-Ford algorithm is another algorithm used to find the shortest distance from a source vertex to all the vertex present in the graph. Bellman-Ford algorithm is slower than Dijkstra algorithm but is considered as a versatile algorithm as it is capable of handling negative weighted graphs as well.

Pseudo code:

Input data:

graph with nodes V and arcs E with weights f(e); source node u. Output data: distances d(v) from the source node u to each node v ∈V.

for eachv∈Vdod(v) := ∞
d(u) = 0

forifrom 1 to |V| - 1:
for eache = (w, v) ∈E:
ifd(v) >d(w) + f(e):
d(v) := d(w) + f(e)

Consider the below diagram:

We will be using Dijkstra’s algorithm to find the shortest distance from vertex V1 to all other.

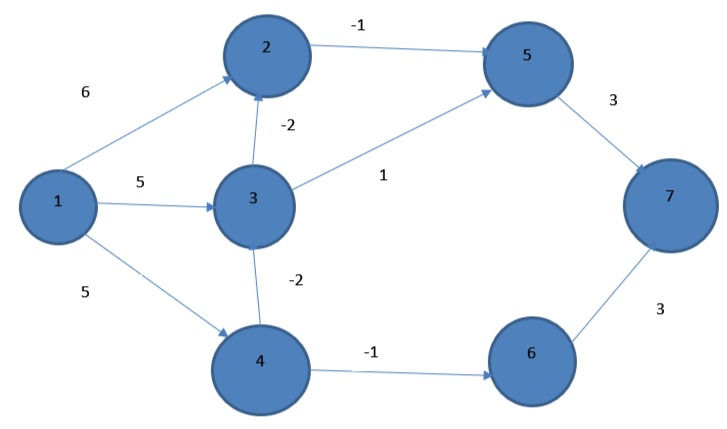
Applying Bellman-Ford algorithm

Step1:

Count the number of vertices in the graph:

Now as in the diagram we can see there are 7 vertices so for this problem every vertex will undergo maximum n-1 relaxation i.e. 7-1=6 relaxation.

Relaxation formula:

If(d[u]+c(u,v)<d[v ])

Then

d[v]= d[u]+c(u,v)

where d[u], d[v] is the weight quantity associated with vertex u and v, c(u,v) is the edge weight between vertex u and v.

Step 2:

Enlist all the edges

(1,2) (1,3) (1,4) (2,5) (3,2) (3,5) (4,3) (4,6) (5,7) (6,7)

Initially all vertices are marked as infinity so

V1	V2	V3	V4	V5	V6	V7
0	∞	∞	∞	∞	∞	∞

Take the first pair (1,2):

So d[u]=d[V1]=0

c(u,v)=c(V1,V2)= 6 and d[v]=d[V1]=∞

Applying relaxation formula

d[u]+c(u,v)<d[v]) i.e. d[V1]+c(V1,V2)<d[V2])

0+6<∞ so the condition satisfies hence replace d[v2] with d[V1]+c(V1,V2) so the table is

V1	V2	V3	V4	V5	V6	V7
0	6	∞	∞	∞	∞	∞

Now repeat the process for all the vertex taking the above table as the reference for updated value.

V1	V2	V3	V4	V5	V6	V7
0	6	3	5	5	4	7

This entire process is counted as one relaxation. Now with the current table repeat the same process five more time to get the final result

2nd relaxation

Repeat the same process again

V1	V2	V3	V4	V5	V6	V7
0	1	3	5	2	4	5

3nd relaxation

V1	V2	V3	V4	V5	V6	V7
0	1	3	5	0	4	3

4th relaxation

V1	V2	V3	V4	V5	V6	V7
0	1	3	5	0	4	3

Now we can observe that 4th and 3rd relaxation are equal so we can stop here.

So, the shortest path of from source V1 to all vertices are

V1->V2=1

V1->V3=3

V1->V4=5

V1->V5=0

V1->V6=4

V1->V7=3

Code Implementation:

// A C++ program for Bellman-Ford's single source
// shortest path algorithm.
#include <bits/stdc++.h>

// a structure to represent a weighted edge in graph
structEdge {
intsrc, dest, weight;
};

// a structure to represent a connected, directed and
// weighted graph
structGraph {
// V-> Number of vertices, E-> Number of edges
intV, E;

// graph is represented as an array of edges.
structEdge* edge;
};

// Creates a graph with V vertices and E edges
structGraph* createGraph(intV, intE)
{
structGraph* graph = newGraph;
graph->V = V;
graph->E = E;
graph->edge = newEdge[E];
returngraph;
}

// A utility function used to print the solution
voidprintArr(intdist[], intn)
{
printf("Vertex Distance from Source\n");
for(inti = 0; i< n; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}

// The main function that finds shortest distances from src to
// all other vertices using Bellman-Ford algorithm. The function
// also detects negative weight cycle
voidBellmanFord(structGraph* graph, intsrc)
{
intV = graph->V;
intE = graph->E;
intdist[V];

// Step 1: Initialize distances from src to all other vertices
// as INFINITE
for(inti = 0; i< V; i++)
dist[i] = INT_MAX;
dist[src] = 0;

// Step 2: Relax all edges |V| - 1 times. A simple shortest
// path from src to any other vertex can have at-most |V| - 1
// edges
for(inti = 1; i<= V - 1; i++) {
for(intj = 0; j < E; j++) {
intu = graph->edge[j].src;
intv = graph->edge[j].dest;
intweight = graph->edge[j].weight;
if(dist[u] != INT_MAX &&dist[u] + weight <dist[v])
dist[v] = dist[u] + weight;
}
}

// Step 3: check for negative-weight cycles. The above step
// guarantees shortest distances if graph doesn't contain
// negative weight cycle. If we get a shorter path, then there
// is a cycle.
for(inti = 0; i< E; i++) {
intu = graph->edge[i].src;
intv = graph->edge[i].dest;
intweight = graph->edge[i].weight;
if(dist[u] != INT_MAX &&dist[u] + weight <dist[v]) {
printf("Graph contains negative weight cycle");
return; // If negative cycle is detected, simply return
}
}

printArr(dist, V);

return;
}

// Driver program to test above functions
intmain()
{
/* Let us create the graph given in above example */
intV = 5; // Number of vertices in graph
intE = 8; // Number of edges in graph
structGraph* graph = createGraph(V, E);

// add edge 0-1 (or A-B in above figure)
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;

// add edge 0-2 (or A-C in above figure)
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;

// add edge 1-2 (or B-C in above figure)
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;

// add edge 1-3 (or B-D in above figure)
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;

// add edge 1-4 (or A-E in above figure)
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;

// add edge 3-2 (or D-C in above figure)
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;

// add edge 3-1 (or D-B in above figure)
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;

// add edge 4-3 (or E-D in above figure)
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;

BellmanFord(graph, 0);

return0;
}

---

Question- 5) Explain All-Pairs Shortest Paths.

Answer: All pair shortest path algorithms are the algorithms that are used to find the shortest distance between all the vertices present within the graph.

There are many all-pairs shortest path algorithms like Johnson's algorithm, Floyd-Warshall algorithm with efficiency in different scenario

Floyd-Warshall algorithm is efficient in dealing with graphs which have all positive weighted graph.

Johnson's algorithm is less efficient than Floyd-Warshall algorithm but it is considered as a versatile algorithm as it can provide result in case of negative weighted graph as well.

---

Question- 6) Explain Floyd-Warshall Algorithm.

Answer: Floyd-Warshall Algorithm is one of the shortest path algorithms used to calculate the shortest path between all pairs of vertices present in the graph. This algorithm works on the dynamic programming approach and is helpful is finding shortest path in a weighted graph with positive as well as negative weights (but with no negative cycles).

The time complexity of this algorithm is O(n3).

Pseudocode:

for i = 1 to N
for j = 1 to N
if there is an edge from i to j
dist[0][i][j] = the length of the edge from i to j
else
dist[0][i][j] = INFINITY

for k = 1 to N
for i = 1 to N
for j = 1 to N
dist[k][i][j] = min(dist[k-1][i][j], dist[k-1][i][k] + dist[k-1][k][j])

Example:

Step 1: Create a matrix D(0) which represent all the weights between all the edges

D(0)= 0171026 ∞ 0

Now consider every vertex as an intermediate node

Consider Vertex 1 as intermediate:

Possible Path: (2-1-3), (3-1-2)

D1(2,3) =min{D0(2,3), D0(2,1) +D0(1,3)}

=min {2,1+7}

=2 i.e., remains unchanged

D1(3,2) =min{D0(3,2), D0(3,1) +D0(1,2)}

=min {∞, 6+4}

=10

10<∞. Hence the previous entry of ∞ for 3rd row and 2nd column is replaced by 10.

D (1) = 0471026100

Consider Vertex 2 as intermediate:

Possible Path: (1-2-3)

D2(1,3) =min{D1(1,3), D1(1,2) +D1(2,3)}

=min {7, 4+2}

=6

6<7. Hence the previous entry of 7 for 1st row and 3rd column is replaced by 6.

D (2) =0461026100

Consider Vertex 3 as intermediate:

Possible path: (2-3-1)

D3(2,1) =min{D2(2,1), D2(2,3) +D2(3,1)}

=min {1,2+6}

=1

i.e., remains unchanged

D (3) = 0461026100

D (3) gives shortest distances between any pair of vertices

Code :

int i, j, k;
// Input data into dist, where dist[i][j] is the distance from i to j.
int dist[N][N]; // For some N

void calculate_all_pairs_shortest_path() {
int i, j, k;
for ( k = 0; k < N; k++ )
for ( i = 0; i< N; i++ )
for ( j = 0; j < N; j++ )
dist[i][j] = min( dist[i][j], dist[i][k] + dist[k][j] );
}

int get_distance(int u, int v) {
return dist[u][v];
}

---

Question- 7) Explain Johnson's Algorithm?

Answer: Johnson's algorithm is another algorithm that can be used to find the shortest distance between all pairs of vertices in a graph. The algorithm is capable of dealing with negative weighted edges as well but the have the limitation that no negative weight cycle may exist.

The algorithm uses Bellman-Ford Algorithm to convert all the negative edges to positive and then apply Dijkstra algorithm to find the minimum distance between all possible pair.

Using Johnson's algorithm, we can find all pair shortest paths in O (V2log V + VE) time . Where V is the number of vertices and E is the number of edges present in the graph.

Pseudo code:

Input: Graph G Output: List of all pair shortest paths for G

Notation:

G=graph

G'=new graph

W= original weight function.

s=new vertex

v=current vertex

Now introduce a new vertex known as Source vertex and connect it with every vertex in the graph and consider weight of every edge as 0.

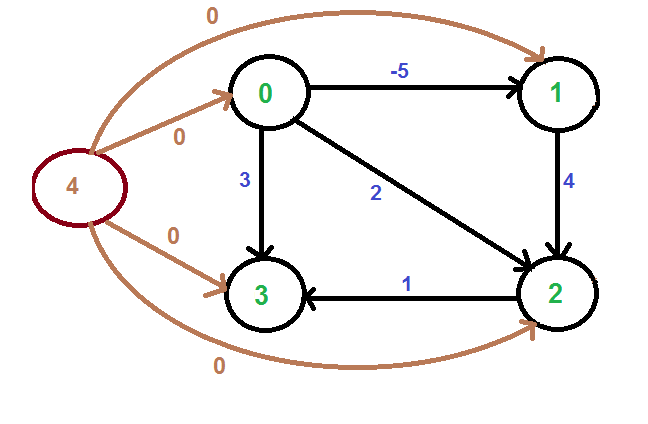
Now apply Bellman-Ford Algorithm

V0	V1	V2	V3	V4
0	∞	∞	∞	∞

All the pair of edges

(4,0) (4,1) (4,2),(4,3),(0,1) (0,2) (0,3) (1,2) (1,3)

V0	V1	V2	V3	V4
0	-5	-1	0	0

Now apply the formula:

w (a, b) = w (a, b) + h (a) - h (b)

For (0,1)

=w (0,1) +h (0)-h (1)

=-5+0-(-5)

=0

For (1,2)

= w (1,2) +h (1)-h (2)

=4+(-5) -(-1)

=0

For (0,2) = w (0,2) +h (0)-h (2)

=2+0-(-1)

=3

For (3,2) = w (3,2) +h (3)-h (2)

=1+0-(-1)

=0

For (0,3) = w (0,3) +h (0)-h (3)

=3+0-(-0)

=3

Now we get all the weights as positive so remove the source and draw the table again.

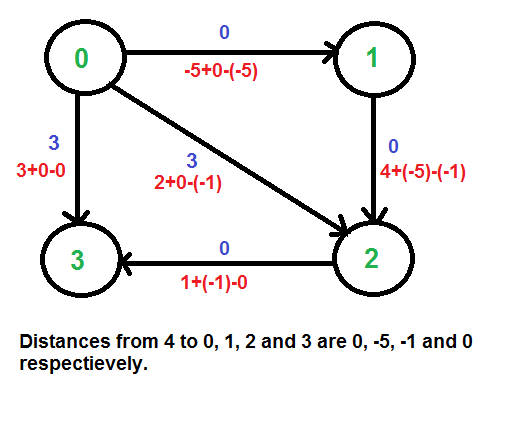
Now apply Dijkstra algorithm to the above diagram

V0	V1	V2	V3
0	∞	∞	∞

The starting node is V0 so explore all node from V0

V0	V1	V2	V3
0	0	3	3

Now among these the smallest one is V1 so select V1. And explore all vertex and if it can relax any vertex with less value than replace that value. We can observe that V2 can be reached through v1 with total weight 0+1=2.

V0	V1	V2	V3
0	0	0	3

Now select V2 and explore all the possibility.

V0	V1	V2	V3
0	0	0	0

So, we find the most optimal solution.

V0->V1	0
V0->V2	0
V0->V3	0
V1->V2	0
V1->V3	0
V3->V4	0

Code Implementation:

#include <iostream>
#include <fstream>
#include <vector>
#include <climits>
#include <exception>
#include <set>

using namespace std;

struct Edge {

int head;
long cost;
};

using Graph = vector<vector<Edge>>;
using SingleSP = vector<long>;
using AllSP = vector<vector<long>>;

const long INF = LONG_MAX;

// first line is in the format <N><M> where N is the number of vertices, M is the number of edges that follow

// each following line represents a directed edge in the form <Source><Dest><Cost>

Graph loadgraph(istream& is) {

Graph g;

int n, m;

is >> n >> m;

cout<< "Graph has " << n << " vertices and " << m << " edges." <<endl;

g.resize(n+1);

while (is) {

int v1, v2, c;

is >> v1 >> v2 >> c;

if (is) {

g[v1].push_back({v2, c});

}

}

return g;

}

Graph addZeroEdge(Graph g) {

// add a zero-cost edge from vertex 0 to all other edges

for (int i = 1; i<g.size(); i++) {

g[0].push_back({i, 0});

}

return g;

}

SingleSPbellmanford(Graph &g, int s) {

vector<vector<long>> memo(g.size()+2, vector<long>(g.size(), INF));

// initialise base case

memo[0][s] = 0;

for (int i = 1; i<memo.size(); i++) {

// compute shortest paths from s to all vertices, with max hop-count i

for (int n = 0; n <g.size(); n++) {

if (memo[i-1][n] < memo[i][n]) {

memo[i][n] = memo[i-1][n];

}

for (auto&e : g[n]) {

if (memo[i-1][n] != INF) {

if (memo[i-1][n] + e.cost< memo[i][e.head]) {

memo[i][e.head] = memo[i-1][n] + e.cost;

}

}

}

}

}

// check if the last iteration differed from the 2nd-last

for (int j = 0; j <g.size(); j++) {

if (memo[g.size()+1][j] != memo[g.size()][j]) {

throw string{"negative cycle found"};

}

}

return memo[g.size()];

}

SingleSPdjikstra(const Graph& g, int s) {

SingleSPdist(g.size(), INF);

set<pair<int,long>> frontier;

frontier.insert({0,s});

while (!frontier.empty()) {

pair<int,long> p = *frontier.begin();

frontier.erase(frontier.begin());

int d = p.first;

int n = p.second;

// this is our shortest path to n

dist[n] = d;

// now look at all edges out from n to update the frontier

for (auto e : g[n]) {

// update this node in the frontier if we have a shorter path

if (dist[n]+e.cost<dist[e.head]) {

if (dist[e.head] != INF) {

// we've seen this node before, so erase it from the set in order to update it

frontier.erase(frontier.find({dist[e.head], e.head}));

}

frontier.insert({dist[n]+e.cost, e.head});

dist[e.head] = dist[n]+e.cost;

}

}

}

return dist;

}

AllSPjohnson(Graph &g) {

// now build "g prime" which is g with a new edge added from vertex 0 to all other edges, with cost 0

Graph gprime = addZeroEdge(g);

// now run Bellman-Ford to get single-source shortest paths from s to all other vertices

SingleSPssp;

try {

ssp = bellmanford(gprime, 0);

} catch (string e) {

cout<< "Negative cycles found in graph. Cannot compute shortest paths." <<endl;

throw e;

}
// no re-weight each edge (u,v) in g to be: cost + ssp[u] - ssp[v].

for (int i = 1; i<g.size(); i++) {

for (auto &e : g[i]) {

e.cost = e.cost + ssp[i] - ssp[e.head];

}

}
// now that we've re-weighted our graph, we can invoke N iterations of Djikstra to find

// all pairs shortest paths

AllSPallsp(g.size());

for (int i = 1; i<g.size(); i++) {

allsp[i] = djikstra(g, i);

}

// now re-weight the path costs back to their original weightings

for (int u = 1; u <g.size(); u++) {

for (int v = 1; v <g.size(); v++) {

if (allsp[u][v] != INF) {

allsp[u][v] += ssp[v] - ssp[u];

}

}

}

return allsp;

---

Previous: Dynamic Programming

Next: Backtracking