Greedy Algorithm: Algorithm Class Notes
- Krishan Kumar Gupta
- May 25, 2022
- 20 min read
Updated: Oct 22, 2022
Mobiprep has created last-minute notes for all topics of Algorithm to help you with the revision of concepts for your university examinations. So let’s get started with the lecture notes on Algorithm.
Our team has curated a list of the most important questions asked in universities such as DU, DTU, VIT, SRM, IP, Pune University, Manipal University, and many more. The questions are created from the previous year's question papers of colleges and universities.
Greedy Algorithm
Question- 1) What is Greedy Algorithm and its properties?
Answer: A greedy algorithm is a simple, intuitive algorithm that is used in optimization problem. The algorithm makes the optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem.
An optimization problem is the problem of finding the best solution from all feasible solutions where the objective function reaches its maximum (or minimum) value. For example, the most profit or the least cost.
In Greedy method the following activities are performed.
First, we select some solution from the input domain.
Then we check whether the solution is feasible or not.
From the set of feasible solutions, a particular solution that satisfies or nearly satisfies the objective of the function. Such a solution is called an optimal solution.
The Greedy method works in stages. At each stage only one input is considered at each time. Based on this input it is decided whether a particular input gives the optimal solution or not.
For a problem with the following properties, we can use the greedy technique:
Greedy Choice Property: This states that a globally optimal solution can be obtained by locally optimal choices.
Optimal Sub-Problem: This property states that an optimal solution to a problem, contains within it, an optimal solution to the sub-problems. Thus, a globally optimal solution can be constructed from locally optimal sub-solutions.
Question- 2) What is the Activity Selection Problem in Greedy Algorithms?
Answer: Activity selection problem is an optimization problem which is used to find the optimal solution to conduct maximum number of nonconflicting activities in a given time frame.
Notation:
s, k=array of start time and end time
k= the index that defines the subproblem Sk that to be solved
n= size of the original problem
Pseudo code:
RECURSIVE-ACTIVITY-SELECTOR (s, f, k, n)
1 m = k+1;
2 while m <=n and s[m] < f [k] // find the first activity in Sk to finish
3 m-m +1
4 if m <=n
5 return {am} Union [ RECURSIVE-ACTIVITY-SELECTOR (s, f, m, n)
6 else return ΦLet's take an example
Consider six activities
Activity | A1 | A2 | A3 | A4 | A5 | A6 |
Start Time | 0 | 3 | 1 | 5 | 5 | 8 |
Finish Time | 6 | 4 | 2 | 9 | 7 | 9 |
Step1:
Arrange it the ascending order of the time required to complete the activity
Activity | A1 | A2 | A3 | A4 | A5 | A6 |
Start Time | 1 | 3 | 0 | 5 | 8 | 5 |
Finish Time | 2 | 4 | 6 | 7 | 9 | 9 |
Step 2:
Now start from the beginning and include all those activities whose finish time is smaller than another activity start time
A3->A2->A5->A6
Maximum four activities can be conduct
Code implementation:
// C++ program for activity selection problem.
// The following implementation assumes that the activities
// are already sorted according to their finish time
#include<stdio.h>
// Prints a maximum set of activities that can be done by a single
// person, one at a time.
// n --> Total number of activities
// s[] --> An array that contains start time of all activities
// f[] --> An array that contains finish time of all activities
void printMaxActivities(int s[], int f[], int n)
{
int i, j;
printf ("Following activities are selected n");
// The first activity always gets selected
i = 0;
printf("%d ", i);
// Consider rest of the activities
for (j = 1; j < n; j++)
{
// If this activity has start time greater than or
// equal to the finish time of previously selected
// activity, then select it
if (s[j] >= f[i])
{
printf ("%d ", j);
i = j;
}
}
}
// driver program to test above function
int main()
{
int s[] = {1, 3, 0, 5, 8, 5};
int f[] = {2, 4, 6, 7, 9, 9};
int n = sizeof(s)/sizeof(s[0]);
printMaxActivities(s, f, n);
return 0;
}
Question- 3) Explain Container loading problem using greedy approach?
Answer: A large ship is to be loaded with containers of cargos. Different containers, although of equal size, will have different weights. We want to find out a way to load the ship with the maximum number of containers, without tipping over the ship.
Example:
1) Find the optimal solution for the following data:
n = 8 | c | w8 | w3 | w1 | w4 | w5 | w2 | w7 | w6 |
| 400 | 20 | 30 | 50 | 80 | 90 | 100 | 150 | 200 |
Solution:
Step1: Sort the Containers in the increasing order
n = 8 | c | w8 | w3 | w1 | w4 | w5 | w2 | w7 | w6 |
| 400 | 20 | 30 | 50 | 80 | 90 | 100 | 150 | 200 |
Step 2: Select the containers with minimum weight
(i) 1st minimum Container 20
Remaining weight = 400-20 (20<=400) (T)
= 380
(ii) 2nd minimum Container 30
Remaining weight = 380-30 (30<=380) (T)
= 350
(iii) 3rd minimum Container 50
Remaining weight = 350-50 (50<=350) (T)
= 300
(iv) 4th minimum Container 80
Remaining weight = 300-80 (80<=300) (T)
= 220
(v) 5th minimum Container 90
Remaining weight = 220-90 (90<=220) (T)
= 130
(vi) 6th minimum Container 100
Remaining weight = 130-100 (100<=130) (T)
= 30
Now if we select the next container of weight 150 then it would exceed the capacity.
Optimal Solution Set
[x1, x2, x3, x4, x5, x6, x7, x8] = [1,1,1,1,1,0,0,1]
Question- 4) Explain Travelling Salesperson Problem?
Answer: Travelling Salesman problem is one of the computational problems that can be solved by using a greedy approach.
The problem states that you have a number of places to visit and you know the cost or distance of all possible pairs. The traveler has to visit every place exactly once and come back to the initial place at the end that also only in such a way that the cost or distance covered is minimized.
Notation
S = set of all cities
C=cost to travel all cities from all possible points
Pseudo code
C ({1}, 1) = 0
for s = 2 to n do
for all subsets S Є {1, 2, 3, … , n} of size s and containing 1
C (S, 1) = ∞
for all j Є S and j ≠1
C (S, j) = min {C (S – {j}, i) + d(i, j) for i Є S and i ≠j}
Return minj C ({1, 2, 3, …, n}, j) + d(j, i)Consider an example
A B C D
A. {-1, 10, 15, 20}
B. {10, -1, 35, 25}
C. {15, 35, -1, 30}
D. {20, 25, 30, -1}
We are trying to find out the path/route with the minimum cost such that our aim of visiting all cities once and return back to the source city is achieved. The path through which we can achieve that, can be represented as 1 -> 2 -> 4 -> 3 -> 1. Here, we started from city 1 and ended on the same visiting all other cities once on our way. The cost of our path/route is calculated as follows:
A -> B = 10
B-> D = 25
D -> C = 30
C -> A = 15
Hence, total cost = 10 + 25 + 30 + 15 = 80
Code implementation:
// C# program for the above approach
using System;
using System.Collections.Generic;
class TSPGreedy{
// Function to find the minimum
// cost path for all the paths
static void findMinRoute(int[,] tsp)
{
int sum = 0;
int counter = 0;
int j = 0, i = 0;
int min = int.MaxValue;
List<int> visitedRouteList = new List<int>();
// Starting from the 0th indexed
// city i.e., the first city
visitedRouteList.Add(0);
int[] route = new int[tsp.Length];
// Traverse the adjacency
// matrix tsp[,]
while (i < tsp.GetLength(0) &&
j < tsp.GetLength(1))
{
// Corner of the Matrix
if (counter >= tsp.GetLength(0) - 1)
{
break;
}
// If this path is unvisited then
// and if the cost is less then
// update the cost
if (j != i &&
!(visitedRouteList.Contains(j)))
{
if (tsp[i, j] < min)
{
min = tsp[i, j];
route[counter] = j + 1;
}
}
j++;
// Check all paths from the
// ith indexed city
if (j == tsp.GetLength(0))
{
sum += min;
min = int.MaxValue;
visitedRouteList.Add(route[counter] - 1);
j = 0;
i = route[counter] - 1;
counter++;
}
}
// Update the ending city in array
// from city which was last visited
i = route[counter - 1] - 1;
for(j = 0; j < tsp.GetLength(0); j++)
{
if ((i != j) && tsp[i, j] < min)
{
min = tsp[i, j];
route[counter] = j + 1;
}
}
sum += min;
// Started from the node where
// we finished as well.
Console.Write("Minimum Cost is : ");
Console.WriteLine(sum);
}
// Driver Code
public static void Main(String[] args)
{
// Input Matrix
int[,] tsp = { { -1, 10, 15, 20 },
{ 10, -1, 35, 25 },
{ 15, 35, -1, 30 },
{ 20, 25, 30, -1 } };
// Function call
findMinRoute(tsp);
}
}
Question- 5) Explain coin exchange problems using a greedy approach?
Answer: You have given an amount M and you want to change for that value and you have infinite supply of each of the denomination in Indian Currency(let's consider) i.e. {1,2,5,10,20,50,100,500,2000) valued notes and coins so we need to find out what is the minimum number of notes required to make the change equals to the given value M.
Pseudo code:
COIN-CHANGE-GREEDY(n) //n is the input value i.e. the value whose change needs to be calculated
coins = [20, 10, 5, 1]
i = 0
while (n)
if coins[i] > n
i++
else
print coins[i]
n = n-coins[i]Let's take an example to understand it better
Suppose you have amount =181 and you want to convert it into change
Step 1:
Find the denomination which is nearer but smaller to the given number from the given denomination set. In this case it is 100.
Step 2:
Create an empty array and add 100 in the array now subtract 100 from the amount 181-100= 81. Now repeat steps 1 and 2 until you get an amount as zero.
So Arr={100}
81 -50=31
Arr={100,50}
31-20=11
Arr={100,50,20}
11-10=1
Arr= {100,50,20,10}
1 – 1 =0
Arr= {100,50,20,10,1}
So, for 181 the change with minimum notes/coin is 5
Code implementation:
// C++ program to find minimum
// number of denominations
#include <bits/stdc++.h>
using namespace std;
// All denominations of Indian Currency
int deno[] = { 1, 2, 5, 10, 20,
50, 100, 500, 1000 };
int n = sizeof(deno) / sizeof(deno[0]);
void findMin(int V)
{
sort(deno, deno + n);
// Initialize result
vector<int> ans;
// Traverse through all denomination
for (int i = n - 1; i >= 0; i--) {
// Find denominations
while (V >= deno[i]) {
V -= deno[i];
ans.push_back(deno[i]);
}
}
// Print result
for (int i = 0; i < ans.size(); i++)
cout << ans[i] << " ";
}
// Driver program
int main()
{
int n = 93;
cout << "Following is minimal"
<< " number of change for " << n
<< ": ";
findMin(n);
return 0;
}Question- 6) Explain Dijkstra's Algorithm?
Answer: Dijkstra's Algorithm is a shortest path algorithm used to find the shortest path from source to all the possible vertices present in the graph. The algorithm used a greedy approach to solve this problem. It is one of the most efficient algorithms but is not efficient to deal with negative weighted graph
The time complexity for all V vertices is V * (E*logV) i.e O(VElogV).
Notation:
G =Weighted directed graph
S= Set of vertices
w (u, v) = the weight
Pseudo code:
of the edge between u and v
s=source vertex
DIJKSTRA (G, w, s)
Initialize-single source (G, s)
S=Φ
Q=G.V
While Q != Φ
U=EXTRACT-MIN(Q)
S=S U {u}
for each vertex v € G.Adj[u]
RELAX(u,v,w)Consider the below graph:
We will be using Dijkstra's algorithm to find the shortest distance from vertex V1 to all other.
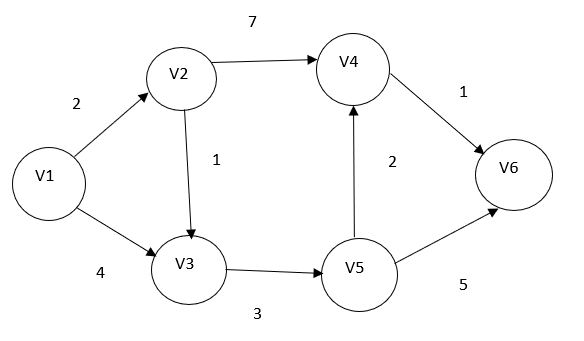
V1 | V2 | V3 | V4 | V5 | V6 |
0 | ∞ | ∞ | ∞ | ∞ | ∞ |
As our starting vertex is V1 so choose V1 and explore all the possible vertex that can be accessed through V1
V2 | V3 | V4 | V5 | V6 |
2 | 4 | ∞ | ∞ | ∞ |
Now among these the smallest one is V2 so select V2. And explore all vertex and if it can relax any vertex with less value than replace that value. We can observe that V3 can be reached through v2 with total weight 2+1=3
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 9 | ∞ | ∞ |
Now select V2
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 9 | 6 | ∞ |
Now Select the minimum in all unselected vertex.
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 8 | 6 | 11 |
Now select V4
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 8 | 6 | 11 |
Now select V4
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 8 | 6 | 9 |
Now select 6
V2 | V3 | V4 | V5 | V6 |
2 | 3 | 8 | 6 | 9 |
So, the result is
Vertex | Distance |
V2 | 2 |
V3 | 3 |
V4 | 8 |
V5 | 6 |
V6 | 9 |
Code Implementation:
// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
#include <limits.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 9
// A utility function to find the vertex with minimum distance value, from
// the set of vertices not yet included in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// A utility function to print the constructed distance array
void printSolution(int dist[])
{
printf("Vertex \t\t Distance from Source\n");
for (int i = 0; i < V; i++)
printf("%d \t\t %d\n", i, dist[i]);
}
// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
int dist[V]; // The output array. dist[i] will hold the shortest
// distance from src to i
bool sptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i] = false;
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices not
// yet processed. u is always equal to src in the first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an edge from
// u to v, and total weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
&& dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist);
}
// driver program to test above function
int main()
{
/* Let us create the example graph discussed above */
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
Question- 7) What do you understand by Minimum spanning tree?
Answer: A Minimum Spanning Tree (MST) is a subgraph of an undirected graph such that the subgraph spans (includes) all nodes, is connected, is acyclic, and has minimum total edge weight. A minimum spanning tree is the network with the lowest total cost.
Question- 8) Explain Prim's minimum spanning tree for adjacency list representation.
Answer: Prim's algorithm uses a greedy approach to find the minimum cost spanning tree. Prim's algorithm shares a similarity with the shortest path first algorithm.
Prim's algorithm treats the nodes as a single tree and keeps on adding new nodes to the spanning tree from the given graph.
Notation:
the connected graph G and the
root r of the minimum spanning tree
w is the weight of edge
PSEUDO CODE
MST-PRIM(G, w, r)
1 for each u € G.V
2 u.key =∞
3 u.Ï€ = NIL
4 r.key = 0
5 Q = G.V
6 while Q ≠ϕ
7 u = EXTRACT-MIN(Q)
8 for each v€ G.Adj[u]
9 if v € Q and w(u,v) < v.key
10 v. π =u
11 v.key= w(u,v)Let’s understand this with the help of an example
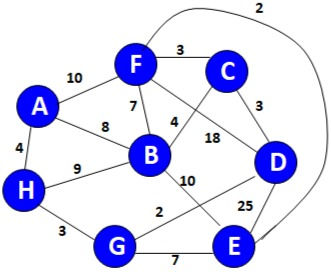
Remove any self loop present in the graph and consider any node as a starting node. Let’s consider G no among all the connection from D find the minimum i.e. G as D to G weight is 2 so connect G to D.
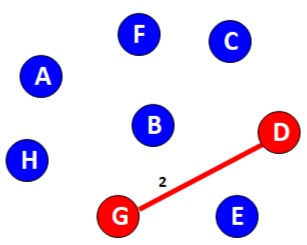
Now check all the possible edges from G and D and choose the minimum one.
*Do not consider any edge whose selection will form a closed loop within the graph.
So
D-G
D-C
C-F
F-E
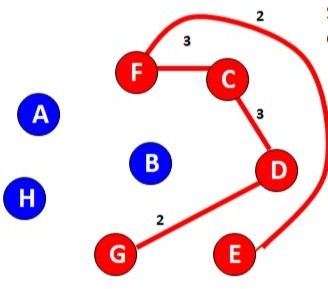
G-H
H-A
C-B
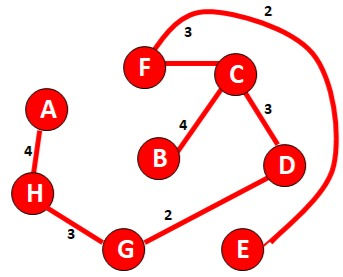
So, to calculate the value add the weights of all selected edges
4+3+2+3+4+3+2=21
Code implementation:
// A C++ program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
void printMST(int parent[], int graph[V][V])
{
cout<<"Edge \tWeight\n";
for (int i = 1; i < V; i++)
cout<<parent[i]<<" - "<<i<<" \t"<<graph[i][parent[i]]<<" \n";
}
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
// Array to store constructed MST
int parent[V];
// Key values used to pick minimum weight edge in cut
int key[V];
// To represent set of vertices included in MST
bool mstSet[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first vertex.
key[0] = 0;
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V - 1; count++)
{
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of
// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// print the constructed MST
printMST(parent, graph);
}
// Driver code
int main()
{
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}
Question- 9) Explain Kruskal's algorithm?
Answer: A greedy technique which continually selects the edges in order of smallest weight and accepts an edge if it does not cause a cycle. This algorithm works with edges, rather than nodes. It maintains a forest, a collection of trees. Initially there are |V| single node tree. Adding an edge merges two trees into one.
When the algorithm terminates, there is only one tree, and this is the minimum spanning tree.
Notation:
G is the connected graphs
W is an array of weights of the edges,
Pseudo code:
MST-KRUSKAL(G, w)
A = Φ ;
for each vertex v€ G.V
MAKE-SET(v)
sort the edges of G:E into nondecreasing order by weight w
for each edge (u,v) € G.E, taken in nondecreasing order by weight
if FIND-SET(u) ≠FIND-SET(v)
A =A U {(u,v)}
return ALet's take an example
Consider the graph
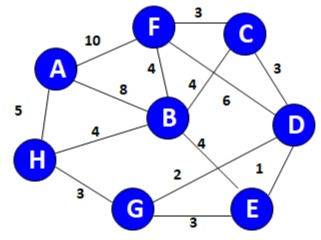
Select arrange all the possible combination in increasing order of their weights
Edge | dv | |
(D,E) | 1 | |
(D,G) | 2 | |
(E,G) | 3 | |
(C,D) | 3 | |
(G,H) | 3 | |
(C,F) | 3 | |
(B,C) | 4 | |
Edge | dv | |
(D,E) | 1 | |
(D,G) | 2 | |
(E,G) | 3 | |
(C,D) | 3 | |
(G,H) | 3 | |
(C,F) | 3 | |
(B,C) | 4 | |
Now select start selecting edges with minimum value and continue to do so until all vertex got connected.
Note:
Ignore those edges whose selection introduces a closed loop in the graph.
D-E
D-G
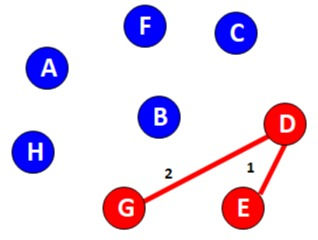
Now next is E-G but if we consider E-G there will be a closed loop so ignore this edge and move ahead.
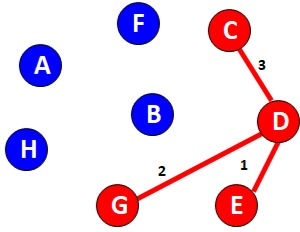
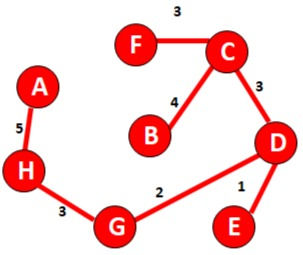
To calculate the value add the weights of all selected edges
5+3+2+1+3+4+3 =21
Code implementation:
// C# Code for above approach
using System;
class Graph
{
// A class to represent a graph edge
class Edge : IComparable<Edge>
{
public int src, dest, weight;
// Comparator function used for sorting edges
// based on their weight
public int CompareTo(Edge compareEdge)
{
return this.weight - compareEdge.weight;
}
}
// A class to represent a subset for union-find
public class subset
{
public int parent, rank;
};
int V, E; // V-> no. of vertices & E->no.of edges
Edge[] edge; // collection of all edges
// Creates a graph with V vertices and E edges
Graph(int v, int e)
{
V = v;
E = e;
edge = new Edge[E];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
// A utility function to find set of an element i
// (uses path compression technique)
int find(subset[] subsets, int i)
{
// find root and make root as
// parent of i (path compression)
if (subsets[i].parent != i)
subsets[i].parent = find(subsets,
subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of
// two sets of x and y (uses union by rank)
void Union(subset[] subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of
// high rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root
// and increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// The main function to construct MST
// using Kruskal's algorithm
void KruskalMST()
{
Edge[] result = new Edge[V]; // This will store the resultant MST
int e = 0; // An index variable, used for result[]
int i = 0; // An index variable, used for sorted edges
for (i = 0; i < V; ++i)
result[i] = new Edge();
// Step 1: Sort all the edges in non-decreasing
// order of their weight. If we are not allowed
// to change the given graph, we can create
// a copy of array of edges
Array.Sort(edge);
// Allocate memory for creating V ssubsets
subset[] subsets = new subset[V];
for (i = 0; i < V; ++i)
subsets[i] = new subset();
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0; // Index used to pick next edge
// Number of edges to be taken is equal to V-1
while (e < V - 1)
{
// Step 2: Pick the smallest edge. And increment
// the index for next iteration
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
// If including this edge does't cause cycle,
// include it in result and increment the index
// of result for next edge
if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
// Else discard the next_edge
}
// print the contents of result[] to display
// the built MST
Console.WriteLine("Following are the edges in " +
"the constructed MST");
for (i = 0; i < e; ++i)
Console.WriteLine(result[i].src + " -- " +
result[i].dest + " == " + result[i].weight);
Console.ReadLine();
}
// Driver Code
public static void Main(String[] args)
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 10;
// add edge 0-2
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 6;
// add edge 0-3
graph.edge[2].src = 0;
graph.edge[2].dest = 3;
graph.edge[2].weight = 5;
// add edge 1-3
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 15;
// add edge 2-3
graph.edge[4].src = 2;
graph.edge[4].dest = 3;
graph.edge[4].weight = 4;
graph.KruskalMST();
}
}
Question- 10) Explain Knapsack algorithm with the help of an explain.
Answer: The knapsack problem is an example of a combinatorial optimization problem. In the knapsack problem, the given items have two attributes at minimum an item's value, which affects its importance, and an item's weight or volume, which is its limitation aspect. Since an exhaustive search is not possible, one can break the problems into smaller subproblems and run it recursively. This is called an optimal substructure.
0/1Knapsack
0/1Knapsack algorithms when used with a greedy approach do not always provide an optimal solution. Consider an example to understand it better
Pseudo code:
// Input:
// Values (stored in array v)
// Weights (stored in array w)
// Number of distinct items (n)
// Knapsack capacity (W)
// NOTE: The array "v" and array "w" are assumed to store all relevant values starting at index 1.
for j from 0 to W do:
m[0, j] := 0
for i from 1 to n do:
for j from 0 to W do:
if w[i] > j then:
m[i, j] := m[i-1, j]
else:
m[i, j] := max(m[i-1, j], m[i-1, j-w[i]] + v[i])
Selection criteria: Maximum beneficial item S = { ( item1 , 5, $70 ), (item2 ,10, $90 ), ( item3, 25, $140 ) }, W=25 (capacity)

As per greedy approach item 3 provides the maximum so we fill the bag with item 3 but this is not the optimal solution as the combination of item 1 and item 2 produces a larger profit of 140.
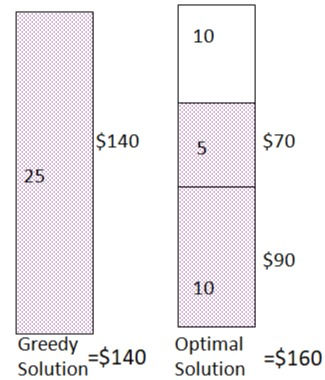
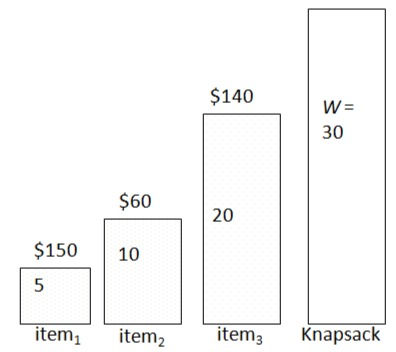
Selection criteria: Minimum weight item
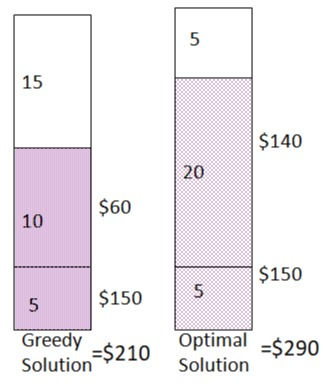
S = { ( item1 , 5, $150 ), (item2 ,10, $60 ), ( item3, 20, $140 ) },
W=30 (capacity)
As per greedy approach item 3+ item 2 sum have the least weights of all existing pairs and produces a profit of 210 but this is not the optimal solution as the combination of item 3+ item 2 produces a larger profit of 290.
Code implementation:
/* A Naive recursive implementation of
0-1 Knapsack problem */
#include <bits/stdc++.h>
using namespace std;
// A utility function that returns
// maximum of two integers
int max(int a, int b) { return (a > b) ? a : b; }
// Returns the maximum value that
// can be put in a knapsack of capacity W
int knapSack(int W, int wt[], int val[], int n)
{
// Base Case
if (n == 0 || W == 0)
return 0;
// If weight of the nth item is more
// than Knapsack capacity W, then
// this item cannot be included
// in the optimal solution
if (wt[n] > W)
return knapSack(W, wt, val, n - 1);
// Return the maximum of two cases:
// (1) nth item included
// (2) not included
else
return max(
val[n] + knapSack(W - wt[n],
wt, val, n - 1),
knapSack(W, wt, val, n - 1));
}
// Driver code
int main()
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
cout << knapSack(W, wt, val, n);
return 0;
}
Question- 11) Explain Fractional Knapsack Problem?
Answer: Fractional knapsack is an algorithm which allows a fraction of an item in order to maximize the value. Now if there is no space to put the entire item into the bag (let’s consider) then it can keep a fraction of that item in order to fill the remaining space thus becoming a more efficient algorithm.
Pseudo code
Fractional Knapsack (Array W, Array V, int M)
for i <- 1 to size (V)
calculate cost[i] <- V[i] / W[i]
Sort-Descending (cost)
i ← 1
while (i <= size(V))
if W[i] <= M
M ← M – W[i]
total ← total + V[i];
if W[i] > M
i ← i+1
Example:n=3, W=20, ( p1,p2,p3)=(25,24,15) and (w1,w2,w3)= (18,15,10).
Item (xi) | Weight (wi) | Profit (pi) |
1 | 18 | 25 |
2 | 15 | 24 |
3 | 10 | 15 |
Now we will calculate profit per unit of that item
Item (xi) | Weight (wi) | Profit (pi) | pi/ wi |
1 | 18 | 25 | 1.38 |
2 | 15 | 24 | 1.6 |
3 | 10 | 15 | 1.5 |
Sort them in ascending order
Item (xi) | Weight (wi) | Profit (pi) | pi/ wi |
1 | 18 | 25 | 1.38 |
2 | 15 | 24 | 1.6 |
3 | 10 | 15 | 1.5 |
The bag capacity is 20 and we know item 2 is providing maximum profit so we will first fill the bag with item 2.
So,
Based on the maximum profit / unit weight
Item (xi) | Weight (wi) | Profit (pi) | pi/ wi |
2 | 15 | 24 | 1.6 |
3 | 10 | 15 | 1.5 |
1 | 18 | 25 | 1.38 |
∑xipi =x2*p2 + x3*p3
= 1*24 + 5/10 *15
= 24 + 7.5
= 31.5
The optimal solution set for this problem is (0,1,1/2) with 31.5 profit.
Code implementation:
// C/C++ program to solve fractional Knapsack Problem
#include <bits/stdc++.h>
using namespace std;
// Structure for an item which stores weight and corresponding
// value of Item
struct Item
{
int value, weight;
// Constructor
Item(int value, int weight) : value(value), weight(weight)
{}
};
// Comparison function to sort Item according to val/weight ratio
bool cmp(struct Item a, struct Item b)
{
double r1 = (double)a.value / a.weight;
double r2 = (double)b.value / b.weight;
return r1 > r2;
}
// Main greedy function to solve problem
double fractionalKnapsack(int W, struct Item arr[], int n)
{
// sorting Item on basis of ratio
sort(arr, arr + n, cmp);
// Uncomment to see new order of Items with their ratio
/*
for (int i = 0; i < n; i++)
{
cout << arr[i].value << " " << arr[i].weight << " : "
<< ((double)arr[i].value / arr[i].weight) << endl;
}
*/
int curWeight = 0; // Current weight in knapsack
double finalvalue = 0.0; // Result (value in Knapsack)
// Looping through all Items
for (int i = 0; i < n; i++)
{
// If adding Item won't overflow, add it completely
if (curWeight + arr[i].weight <= W)
{
curWeight += arr[i].weight;
finalvalue += arr[i].value;
}
// If we can't add current Item, add fractional part of it
else
{
int remain = W - curWeight;
finalvalue += arr[i].value * ((double) remain / arr[i].weight);
break;
}
}
// Returning final value
return finalvalue;
}
// driver program to test above function
int main()
{
int W = 50; // Weight of knapsack
Item arr[] = {{60, 10}, {100, 20}, {120, 30}};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Maximum value we can obtain = "
<< fractionalKnapsack(W, arr, n);
return 0;
}
Question- 12) What is the difference between 0/1 knapsack and fractional knapsack?
Answer:
0/1 knapsack: In the 0/1 knapsack algorithm we either take the entire item or we do not. There is no provision of taking a fraction of the item which wastes the space which remain empty due to the reason that no item fits completely in that space.
Fractional knapsack: Fractional knapsack is an algorithm which allows a fraction of an item in order to maximize the value. Now if there is no space to put the entire item into the bag (let’s consider) then it can keep a fraction of that item in order to fill the remaining space thus becoming a more efficient algorithm.



.png)



Comments